차원 축소

차원 축소가 필요한 이유

차원 축소를 위한 접근 방법

ex) 3d 공간 안에 있는 저차원 부분 공간 subspace이 있는데 여기에 수직¹ 투영하면 평면에 투영된 좌표를 얻음.
ex) 아래 그림 처럼 부분 공간 subspace가 휘어있기도 함.(swiss roll 예제) 오른쪽은 왼쪽의 스위스 롤을 펼쳐서 2D 데이터 셋을 얻은 것임.

\(\star\) 2D 매니폴드는 곡선, 3D 매니폴드는 곡면이라 생각

PCA

PCA is a statistical technique for reducing the dimensionality of a dataset.

분산이 최대로 보존되는 차원 축소가 정보를 가장 적게 손실되어 합리적으로 보임

분산이 큰 순서대로 차원의 수만큼 찾음

i번째 축 = 주성분 PC principal component

이론 : \(X_{n \times m} = U_{n \times n} D_{n \times m} (V_{m \times m})^\top\)
- ver 1 = \(U, V\)가 모두 직교 행렬
- ver 2 = \(U\) 또는 \(V\)가 직교 행렬
왜?
- 데이터 매트릭스 \(X\)가 존재할때 정보는 유지하면서 비용을 줄이는 \(Z\)⁴를 찾고 싶다.
- \(Z\) 구하는 법
  - \(Z = \tilde{U} \tilde{D}\) \(\to\) \(\tilde{U} \tilde{D} = X\tilde{V}\) \(\to\) \(Z = X\tilde{V}\)
  - \(X^\top X = \psi \lambda \psi^\top\)을 구해서 \(Z = X\tilde{\psi}\) \(\to\) \(\hat{X} = Z\tilde{\psi}^\top\)

\(\star\) PCA는 데이터셋의 평균이 0이라고 가정

\(X_{d-proj,n \times d} = X_{n \times M} W_{d,n \times d}\)

설명된 분산의 비율 explained variance ratio

차원 수를 임의로 정하는 것보다는 충분한 분산⁵이 될 떄까지 선택

중요한 특징만을 살리기 위해 PCA를 시도하여 차원 축소하였다.

이후 원본 데이터로 돌아가려 할 때 특징은 살아있지만 완벽히 데이터셋이 일치하지 않는데,

여기서 이 오류를 재구성 오차 = 재건 오류 reconstruction error 라고 한다.

\(X_{n \times M} = X_{d-proj,n \times d} (W_{d,n \times d})^\top\)

차원 축소를 통해 비선형 투영 수행

\(\zeta = \Psi \alpha\)

이 때, \(||\alpha_j|| = 1\)로 정규화한다.
그러기 위해 \(\alpha_j\)를 \(||\zeta_j||\)로 나누어 정규화
- \(||\zeta_j|| = \sqrt{\lambda}_j\)
- \(\alpha_j \to \frac{1}{\sqrt{\lambda}_j} \alpha_j, j=1, \dots, m\)

특징 벡터로 내적하여 나오는 커널\(K\) 행렬로 중심화

\(\alpha\) 정규화 한 후 중심화하면

\((z_1, \dots, z_n) = (\frac{1}{\sqrt{\lambda_1}} \alpha_1,\dots , \frac{1}{\sqrt{\lambda_m}}\alpha_m)^\top HKH\)

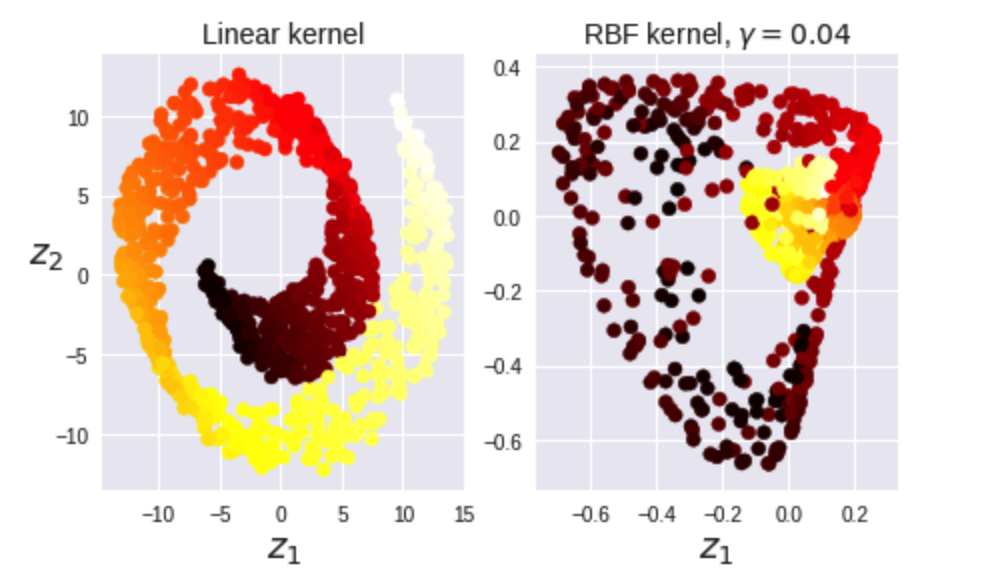
\(\star\) 고유벡터

선형 \(C = \psi \psi^\top\)
비선형 \(K = \psi^\top \psi\)
- \(\psi\)의 길이에 따라 고유값 문제의 표현을 다르게 하여 계산 시간 줄이기
- 차원 수가 표본 수보다 큰 경우에는 커널 행렬을 사용하는 것이 효율적